What is RAID configuration in Windows
RAID Configuration
Learn about Intel RAID configuration. It includes all the RAID levels with diagram, very useful for to clear doubts for layman.
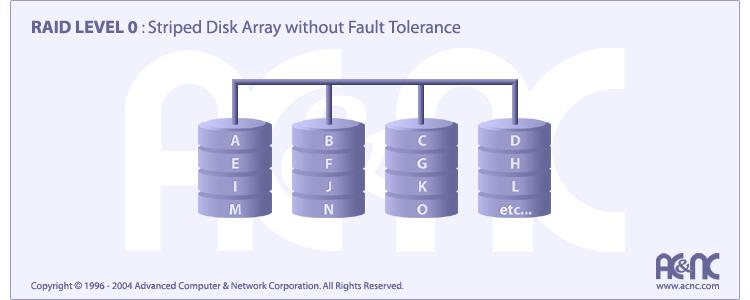
RAID Level 0 requires a minimum of 2 drives to implement
Characteristic & Advantages
RAID 0 implements a striped disk array, the data is broken down into blocks and each block is written to a separate disk drive.
I/O performance is greatly improved by spreading the I/O load across many channels and drives.
Best performance is achieved when data is striped across multiple controllers with only one drive per controller.
No parity calculation overhead is involved.Very simple design & Easy to implement.
Not a “True” RAID because it is NOT fault-tolerant
The failure of just one drive will result in all data in an array being lost &Should never be used in mission critical environments
Disadvantages
Not a “True” RAID because it is NOT fault-tolerant.
The failure of just one drive will result in all data in an array being lost
Should never be used in mission critical environments
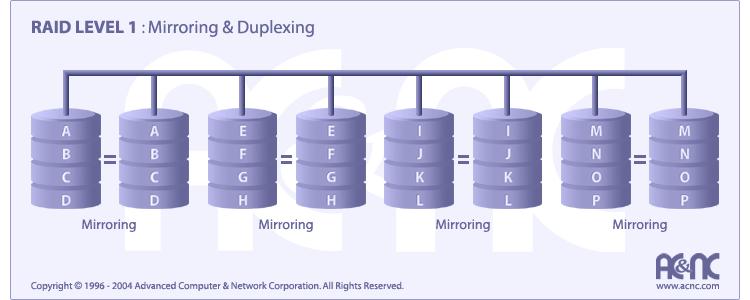
For Highest performance, the controller must be able to perform two concurrent separate
Reads per mirrored pair or two duplicate Writes per mirrored pair. RAID Level 1 requires a minimum of 2 drives to implement.
Characteristic & Advantages
One Write or two reads possible per mirrored pair
Twice the Read transaction rate of single disks, same Write transaction rate as single disks
100% redundancy of data means no rebuild is necessary in case of a disk failure, just a copy to the replacement disk
Transfer rate per block is equal to that of a single disk & Under certain circumstances, RAID 1 can sustain multiple simultaneous drive failures
Simplest RAID storage subsystem design & Highest disk overhead of all RAID types (100%) – inefficient
Typically the RAID function is done by system software, loading the CPU/Server and possibly degrading throughput at high activity levels. Hardware implementation is strongly recommended
May not support hot swap of failed disk when implemented in “software”
Disadvantages
Highest disk overhead of all RAID types (100%) – inefficient
Typically, the RAID function is done by system software, loading the CPU/Server and possibly degrading throughput at high activity levels. Hardware implementation is strongly recommended
May not support hot swap of failed disk when implemented in “software”
Recommended Product
- · Accounting
- · Payroll
- · Financial
- · Any application requiring very high availability.
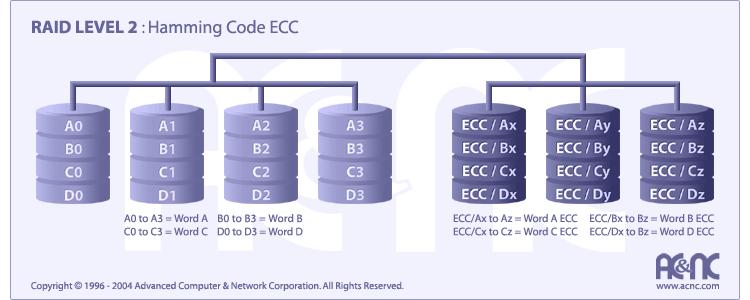
Each bit of data word is written to a data disk drive (4 in this example: 0 to 3). Each data word has its Hamming Code ECC word recorded on the ECC disks. On Read, the ECC code verifies correct data or corrects single disk errors.
Characteristic & Advantages
“On the fly” data error correction
Extremely high data transfer rates possible
The higher the data transfer rate required, the better the ratio of data disks to ECC disks
Relatively simple controller design compared to RAID levels 3,4 & 5
Very high ratio of ECC disks to data disks with smaller word sizes – inefficient
Entry level cost very high – requires very high transfer rate requirement to justify
Transaction rate is equal to that of a single disk at best (with spindle synchronization)
No commercial implementations exist / not commercially viable
Disadvantages
Very high ratio of ECC disks to data disks with smaller word sizes – inefficient
Entry level cost very high – requires very high transfer rate requirement to justify
Transaction rate is equal to that of a single disk at best (with spindle synchronization)
No commercial implementations exist / not commercially viable
The data block is subdivided (“striped”) and written on the data disks. Stripe parity is generated on Writes, recorded on the parity disk and checked on Reads.
RAID Level 3 requires a minimum of 3 drives to implement
Characteristic & Advantages
Very high Read data transfer rate & Very high Write data transfer rate
Disk failure has an insignificant impact on throughput
Low ratio of ECC (Parity) disks to data disks means high efficiency
Disadvantages
Transaction rate equal to that of a single disk drive at best (if spindles are synchronized) Controller design is fairly complex
Very difficult and resource intensive to do as a “software” RAID
Recommended Application
- · Video Production and live streaming
- · Image Editing
- · Video Editing
- · Prepress Applications
- · Any application requiring high throughput
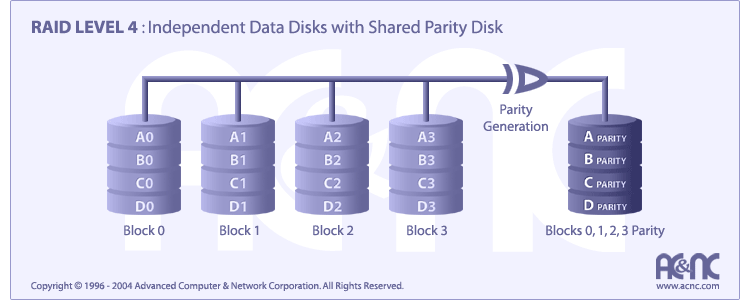
Each entire block is written onto a data disk. Parity for same rank blocks is generated on Writes, recorded on the parity disk and checked on Reads.
RAID Level 4 requires a minimum of 3 drives to implement
Characteristic & Advantages
Very high Read data transaction rate
Low ratio of ECC (Parity) disks to data disks means high efficiency
High aggregate Read transfer rate
Disadvantage
Quite complex controller design
Worst Write transaction rate and Write aggregate transfer rate
Difficult and inefficient data rebuild in the event of disk failure
Block Read transfer rate equal to that of a single disk
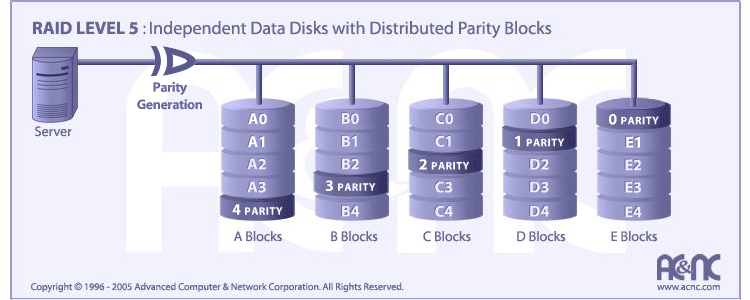
Each entire data block is written on a data disk; parity for blocks in the same rank is generated on Writes, recorded in a distributed location and checked on Reads.
RAID Level 5 requires a minimum of 3 drives to implement
Characteristic & Advantages
Highest Read data transaction rate
Medium Write data transaction rate
Low ratio of ECC (Parity) disks to data disks means high efficiency
Good aggregate transfer rate
Disadvantage
Disk failure has a medium impact on throughput
Most complex controller design
Difficult to rebuild in the event of a disk failure (as compared to RAID level 1)
Individual block data transfer rate same as single disk
Recommended Application
- File and Application servers
- Database servers
- Web, E-mail, and News servers
- Intranet servers
- Most versatile RAID level
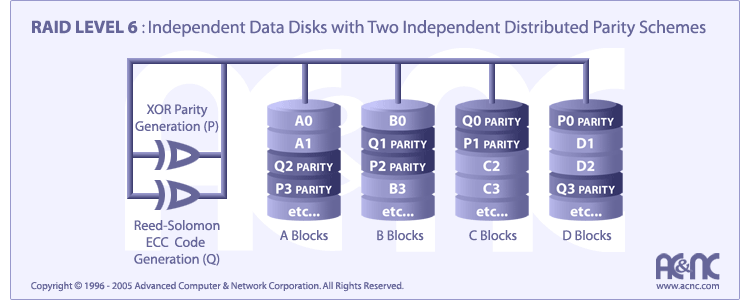
Two independent parity computations must be used in order to provide protection against double disk failure. Two different algorithms are employed to achieve this purpose.
RAID Level 6 requires a minimum of 4 drives to implement
Characteristic & Advantages
RAID 6 is essentially an extension of RAID level 5 which allows for additional fault tolerance by using a second independent distributed parity scheme (dual parity)
Data is striped on a block level across a set of drives, just like in RAID 5, and a second set of parity is calculated and written across all the drives; RAID 6 provides for an extremely high data fault tolerance and can sustain multiple simultaneous drive failures
Perfect solution for mission critical applications
Disadvantage
More complex controller design
Controller overhead to compute parity addresses is extremely high
Write performance can be brought on par with RAID Level 5 by using a custom ASIC for computing Reed-Solomon parity
Requires N+2 drives to implement because of dual parity scheme
Recommended Application
- File and Application servers
- Database servers
- Web and E-mail servers
- Intranet servers
- · Excellent fault-tolerance with the lowest overhead
RAID Level 10 requires a minimum of 4 drives to implement
Characteristic & Advantages
RAID 10 is implemented as a striped array whose segments are RAID 1 arrays
RAID 10 has the same fault tolerance as RAID level 1
RAID 10 has the same overhead for fault-tolerance as mirroring alone
High I/O rates are achieved by striping RAID 1 segments
Under certain circumstances, RAID 10 array can sustain multiple simultaneous drive failures
Excellent solution for sites that would have otherwise gone with RAID 1 but need some additional performance boost
Disadvantage
Very expensive / High overhead
All drives must move in parallel to proper track lowering sustained performance
Very limited scalability at a very high inherent cost
Recommended Application
- Database server requiring high performance
and fault tolerance
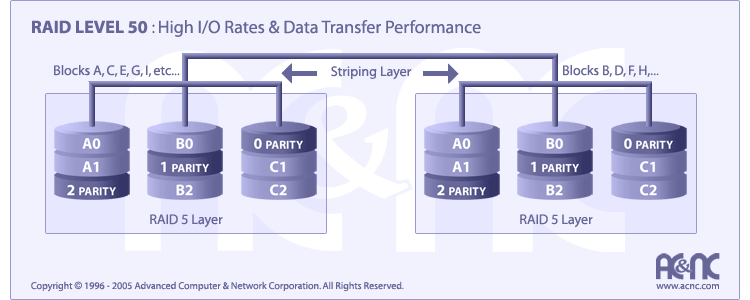
RAID Level 50 requires a minimum of 6 drives to implement
Characteristic & Advantages
RAID 50 should have been called “RAID 03” because it was implemented as a striped (RAID level 0) array whose segments were RAID 3 arrays (during mid-90s)
Most current RAID 50 implementation is illustrated above
RAID 50 is more fault tolerant than RAID 5 but has twice the parity overhead
High data transfer rates are achieved thanks to its RAID 5 array segments
High I/O rates for small requests are achieved thanks to its RAID 0 striping
Maybe a good solution for sites who would have otherwise gone with RAID 5 but need some additional performance boost.
Disadvantages
Very expensive to implement
All disk spindles must be synchronized, which limits the choice of drives.
Failure of two drives in one of the RAID 5 segments renders the whole array unusable
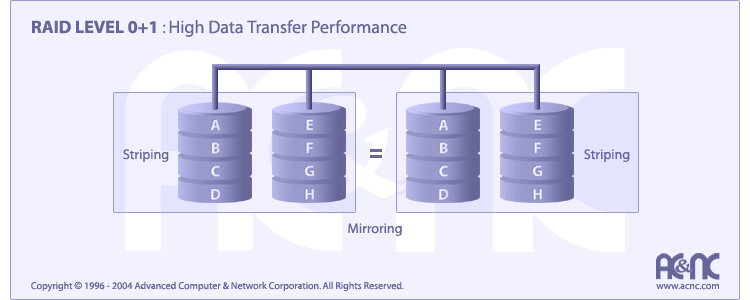
RAID Level 0+1 requires a minimum of 4 drives to implement
Characteristic & Advantages
RAID 0+1 is implemented as a mirrored array whose segments are RAID 0 arrays
RAID 0+1 has the same fault tolerance as RAID level 5
RAID 0+1 has the same overhead for fault-tolerance as mirroring alone
High I/O rates are achieved thanks to multiple stripe segments
Excellent solution for sites that need high performance but are not concerned with achieving maximum reliability
Disadvantage
RAID 0+1 is NOT to be confused with RAID 10. A single drive failure will cause the whole array to become, in essence, a RAID Level 0 array
Very expensive / High overhead
All drives must move in parallel to proper track lowering sustained performance
Very limited scalability at a very high inherent cost
Recommended Application
- Imaging applications
- · General fileserver
Whether you’re looking for troubleshooting tips, deep dives into systems architecture, or the latest in cloud computing, I’m here to help you navigate the evolving tech landscape. Let’s connect, learn, and grow together!
📧 ravi.chopra1709@gmail.com
- Active Directory Group Policy Management: Best Practices - 21 November 2024
- What is Active Directory? A Complete Guide for IT Professionals - 18 November 2024
- Enterprise Virtualization Platforms Comparison: A Technical Deep Dive - 29 October 2024
Good stuff to clear RAID configuration doubts…